【個人用備忘録】QCQI Ch. 12 その1 【No-cloning theorem, Holevo's bound】
文献はもちろん M. A. Nielsen, I. L. Chuang, "Quantum Computation and Quantum Information" (2nd ed.), Cambridge University Press (2010) です. この手の解説は無限にあると思うし,なんなら古い教科書なので最近の発展を一切含まない話なので,私以外の人にとってはこれを読む価値は全くないのですが,アウトプットしようと思わないとすべてを忘れて何も残らない (超重要) ので,ブログに残しておきます.その1は12.1節しかcoverしていません.
No-cloning Theorem
みんな大好きno-cloning theoremです.生まれた時から知っていました (自明な嘘).名前だけ聞くと量子状態はコピーできないのかなという気分になりますが,正確なstatementは,
直交しない2つの状態をコピーできるunitary操作は存在しない より正確に言うと, 任意の直交しない2つの非ゼロの状態
について,(1)
と (2)
の (1), (2) を満たすようなunitary演算子
は存在しない (
は適当な状態).
というものです.これの証明は簡単 (そのようなunitary operationが存在すると思ったときに,ノルムが保存しないから矛盾って言うだけ).注意として,コピーしたい状態を既に知っているならば無限にコピーできるし,コピーしたい状態が例えば「 のどちらかだ」,と知っているときにも可能です.じゃないとCNOT gateとかアウトですからね *1.
これのcorollaryとして,
すべての状態をコピーできるunitary操作は存在しない
が言えます.たぶんこっちが有名.
Holevo’s bound
直交していない状態を完全に区別することができないのは有名ですが,「測定によって状態についてどこまで引き出すことが出来るのか」を定量化したものがHolevo's boundです.
setup
確率 で状態
なるものが送られてくるとき,その状態を測定して,送られてきた状態がどの
かを判別したい.
Holevo’s boundは,「測定によって,どこまで知ることができるか」ということについてupperboundを与えるものです.
「測定結果 から,状態のラベル
について,どこまで知ることができるか」を定量化するために,相互情報量 (mutual information, accessible information)
を定義します.*2 *3
statement
上記のsetupのもとで,次の不等式が成り立ちます
ここで
. *4
この右辺はHolevo χ quantityと呼ばれる量で,量子情報のいろんなところで出てくる量です.
この不等式の右辺がYによっていない (どんな測定をするかによらない) ことが大事で,これにより「どんな測定をしたとしても,得られる情報量はHolevo χ quantityで抑えられてしまう」ことが言えます.
証明はしません.軽いメモという名目なので ブログに書くのがだるいので.測定結果を格納するancilla systemを加えて,quantum mutual informationをstraightforwardに計算すればできた気がします.
直感を養う
statementを述べただけでは「へーそうなんだー」で終わるので直感を養うためにいくつかコメントを加えます.
- von Neumann entropyについて,次の不等式が知られています.(Nielsen-Chuang, Theorem 11.10)
等号成立は
たちがorthogonal supportを持つとき (pure stateなら,状態が直交しているとき)
この不等式とHolevo boundを合わせると, が得られます.
そして等号成立の可能性は, たちがorthogonal supportを持つときに限られます.これはとても直感的で,accessible informationが最大 (
) のとき,「Yを知った後にものこるXの不確かさ」
がゼロになります. この時は,Yが分かればXが完全にわかる,つまり測定から状態の区別ができる,ということになり,それが可能なのは状態が互いに直交している場合に限られるので,この等号成立条件は常識とconsistentになっています.
- 古典的な確率論の話で,確率変数Xから確率変数Yをどれくらいうまく推測できるか,ということに関して,conditional entropyを使った次の不等式が知られています.
Fano不等式
YからのXのguessを
と書き,それが外れている確率を
と書きます.このerror probabilityとconditional entropyについて,次の不等式が成り立ちます.
,
ここで1項目はbinary entropy, 2項目の
はXの要素の数です.
証明はしません.具体例であそんでみると分かるのですが,これはerror probabilityについて,ある種のlower boundを与えています.「Yを知った後にものこるXの不確かさ」 がそれなりにあると,全然正しいguessができないというのはそれはそうという感じです.
自明な変形ですが,次のようにも書き換えられます.
ここから,次のような気持ちが得られて気持ち良くなれます:
χが小さい ↔ accessible information
を大きくできる ↔ 正しいguessができる (
を小さくできる)
χが大きい ↔ accessible information
がどうしても小さい ↔ 正しいguessができない (
を小さくできない)
下書きを抱え込むと永遠にアウトプットしない (超重要) ので,その1はここで区切ります.そのうちその2を書きます.
*1:00 -> 00, 01 -> 11とかやるので,control bitをある種コピーしている
*2: この記事では で古典Shannonエントロピー,
でvon Neumannエントロピーを表すこととします.
*3:なぜこの量が「 から,
について,どこまで知ることができるか」を定量化するのか,ということについては,conditional entropyに書き直すと分かりやすいです.
これは, は「もとからあるXの不確かさ」を,
は「Yを知った後にものこるXの不確かさ」を定量化するものなので,その差分は「Yを知ったことで,不確かさがどれだけ削減されたか」を意味します.これはまさに,「Yを知ったことで,Xについてどれだけ分かったか」を測る量となっています.
*4: は 確率
で状態
を古典的に重ね合わせた状態なので,まさに測定する前の量子状態がこれ
Raspberry Pi clusterでMathematicaを使う
雑記です。コロナ騒ぎでいつも使っていた計算機の使用に"面倒なこと"が増えてしまったので、「自前でクラスター作るチャンスだ!」と思い、試しに試行錯誤した記録を残します。とりあえず方法を知っておくことが目的だったので、Raspberry Pi 4 Model B/4GB *2個で遊んでみました。
参考になるかもしれない文献は
- B. Jacobus and RJ Podeschi, `` Low-cost cluster computing using raspberry pi with mathematica' ', Proceedings of the EDSIG Conference, (2017) ; http://proc.iscap.info/2017/pdf/4363.pdf
です。
Background
Raspberry Pi は安価な手のひらサイズのコンピュータです。素晴らしいことに、Raspberry PiはWolframと提携していて、無料でMathematicaを使うことができます! *1 一方で、Mathematicaは普通にライセンスを入手するととても高い *2。
このような状況にあるので、raspberry pi clusterでmathematicaを使うと低コストでmathematicaの重い計算を回せるかもしれない。
準備
揃えるもの
まずは動くraspberry piを欲しい数だけ揃えます。n個準備したいなら、
- Raspberry Pi 4 RAM 4GB *3 n個
- 電源ケーブル・ヒートシンク・マイクロSDカード*4 n個
- usbマウス・キーボード一式
- micro HDMIから任意の端子へのケーブル(例えばHDMI(A))・その端子が出力できるモニター 1つ
を準備する。*5
ここでは方法を紹介するに留めるので、とりあえず2つ準備します。
VNC: リモートで操作する
n個マウス・キーボード・モニターが準備できればそれでいいのですが、それはむしろコストがかかるので、リモートでPCやタブレットで操作できるようにしておきます。 基本的には
- IP addressを固定する。
- Raspberry PiでVNCを有効にする。
- Real VNCをクライアントに導入する。
をすればよいです。これに関してはよい解説が容易に見つかると思うので、詳しくは省略します。
Passwordless SSH
Mathematicaがデバイスを超えてコマンドを実行するために、SSHの準備をしておきます。*6
クライアント側 (使う方) で公開鍵を生成し、それをサーバー側 (使われる方) に認証させます。相互に認証させ、行き来できるようにします。 あるデバイスを一つ決め (master)、そのデバイスからそのほかの全てのデバイスにログインできるようになっていれば良さそうです。
操作は次の通りです。
- クライアント側でsshキーを作成: "ssh-keygen"を実行 *7 。この際パスワードは入力しない。
- 続けて、home/pi/.sshのディレクトリに公開鍵ファイル id_rsa.pubが生成されていることを確認。*8
- サーバー側のhome/pi/.sshのディレクトリ (無ければ作る) に "authorized_keys" というファイルを作成
- クライアント側で生成したid_rsa.pubの内容をさっき作ったauthorized_keysにコピー。id_rsa.pubに書いてある「ssh-rsa 何たらかんたら」を (2つ目以降なら改行して) authorized_keysにぺたぺた貼り付けます。 *9
- これで準備は完了です。繋がるかテストするには、サーバー側をrebootしたあと、クライアント側から"ssh -i .ssh/id_rsa pi@(サーバー側のipアドレス)"を実行してつないでみるとよいです。 *10
- 上記の操作を、全てのデバイスに対して、
自分自身を除く全てのデバイスの公開鍵をauthorized_keysに書き込むまで繰り返します。あるデバイス (master) の公開鍵をauthorized_keysに書き込むまで繰り返します。
こうしてSSHの準備が整いました。
Mathematica Remote Kernel Configuration
Mathematicaがremote kernelを使えるようにします。操作は次の通りです。
- Mathematicaを立ち上げ、FrontEndTokenExecute["PreferencesDialog"]を実行します。
- Parallel tab -> Remote Kernels -> Enable Remote Kernels -> Add Hostと進みます。

- Host nameにRemoteで使用するraspberry piのipアドレスを入力する。 -> Kernelを4にする。他はデフォルトで良い。-> Enableにチェックを入れる。
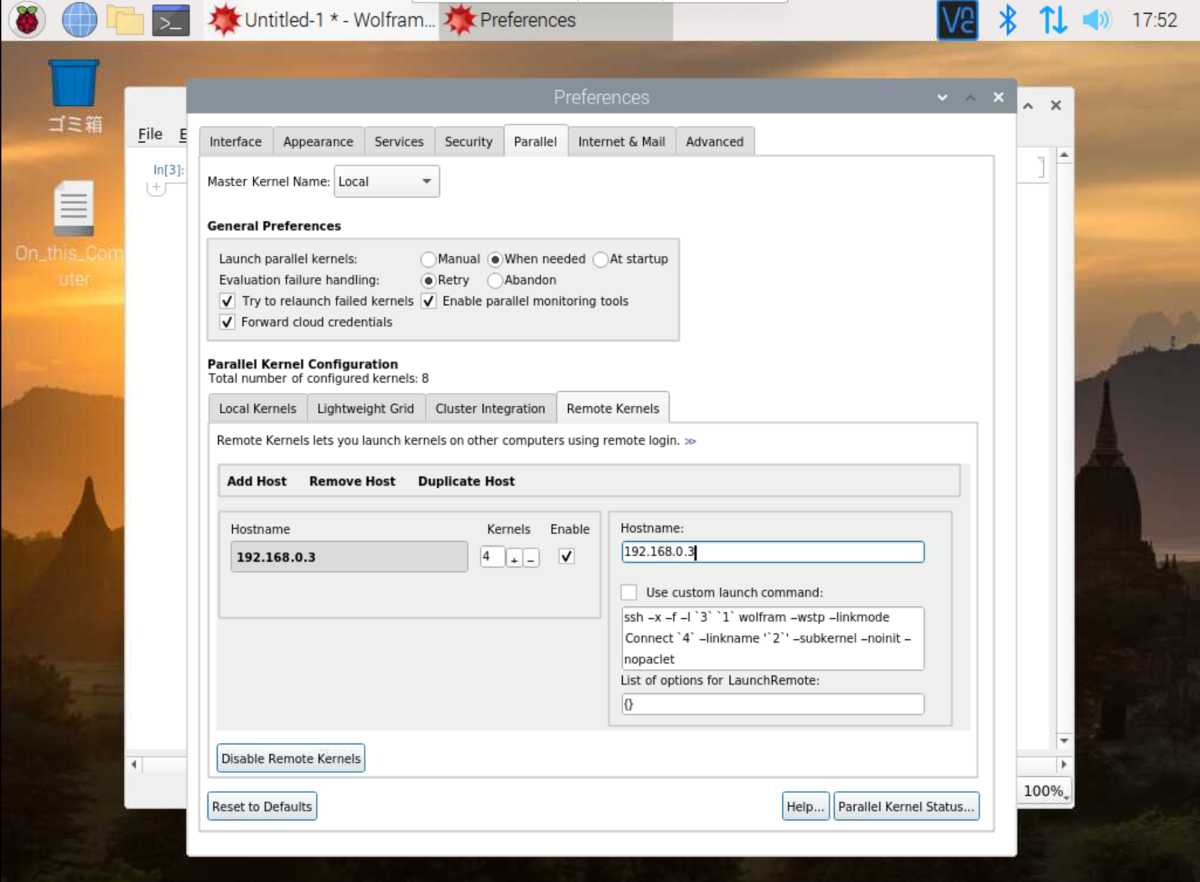
これで終わりです。諸々めんどくさいことは自動でやってくれる!うれしいね!
動かしてみる。
便利なコマンドにParallelCombineなるものがあります。
AbsoluteTimingで時間を測ってあげて、とりあえず素数を104個求めてあげましょう。構成はRaspberry Pi 4 Model B/4GB *2個です。 比較のため、local kernelでの評価も行ってあげます。なのでMathematicaで
AbsoluteTiming[ParallelCombine[Prime,Range[10000]]]
と
AbsoluteTiming[Prime[Range[10000]]]
を行ってみます。すると並列化した方は0.283021 sec、並列化してない方は0.01479 secかかりました。並列化しない方が速い!悲しい!
並列化による通信コストを頭に置いておかないといけないかもしれません。
これで終わってしまうのも悲しいので、素数を106個求めてあげました。結果は並列化した方は2.97868 sec、並列化してない方は7.05872 secで、ちゃんと2倍程度早くなっていました。

Mathematicaの並列計算について、コマンドは公式ドキュメント
を参考にしてください。だいたいParallelize[]関数で全部やってくれそうな気がします。 *11
こうして複数デバイスでの並列化をすることができました。
感想
RPi4は普通に一台で強いので、たくさん買えば結構重い計算を投げることができそうです。 でもRPi 4で遊んでると保冷剤がすぐ溶けてしまう。熱い。
*1:https://www.wolfram.com/raspberry-pi/
*2:https://www.wolfram.com/mathematica/pricing/
*3:記事を書いている時点で最も高スペック。スペックは
Raspberry Pi 4 Model B specifications – Raspberry Pi
参照。記事を書いている途中で8GBのモデルが発売されてしまいました……
*4: Raspbianを入れておく。例えば https://www.kkaneko.jp/tools/raspbian/raspbian_install.html
*5: 探すのがめんどくさい人には、代理店によるスターターキットがある。 https://raspberry-pi.ksyic.com/main/index
*6: 例えば、 https://qiita.com/hinemoss/items/2bdc2293c84bc1001214 などの解説があります。
*7: デフォルトではRSA 2048bit; RSAでない他の暗号化方式を採用する場合は-t optionを使う。
*8: 同時に生成されているid_rsaは秘密鍵なので扱いには注意すること。
*9:セキュリティが不安なら、/etc/hosts.denyと/etc/hosts.allowを編集するなりして、接続可能なipを指定するとよい。
*10:接続しても接続した感がつかめないですが、exitしてみるとどのipからログアウトしたかわかる。
*11:AbsoluteTiming[ParallelCombine[Prime,Range[10000]]]の代わりにAbsoluteTiming[Parallelize[Prime[Range[10000]]]]を実行してもほとんど同じ時間で結果を返してもらえる。